
全部
▼
搜索
熱搜:
位置:中冶有色 >
> 三向正交纖維增強鋁基復(fù)合材料經(jīng)向拉伸漸進損傷及其斷裂力學(xué)行為
 704
編輯:中冶有色技術(shù)網(wǎng)
來源:劉豐華,趙文豪,蔡長春,王振軍,沈高峰,張映鋒,徐志鋒,余歡
704
編輯:中冶有色技術(shù)網(wǎng)
來源:劉豐華,趙文豪,蔡長春,王振軍,沈高峰,張映鋒,徐志鋒,余歡
| Fiber type | d/μm | Tensile strength/MPa | Young's modulus/GPa | Density/g·cm-3 | Elongation/% | Poisson's ratio |
|---|---|---|---|---|---|---|
| M40J | 6 | 4400 | 377 | 1.81 | 0.7 | 0.26 |
| Elements | Si | Mg | Cu | Mn | Ti | Al |
|---|---|---|---|---|---|---|
| Content | 0.3 | 9.5~11.0 | 0.1 | 0.15 | 0.15 | Bal. |
| Fabric structure | Fabric size/mm |
Yarn density /bundle·cm-1 |
Yarn specification |
Fabric weight /kg |
Fiber content/% |
|---|---|---|---|---|---|
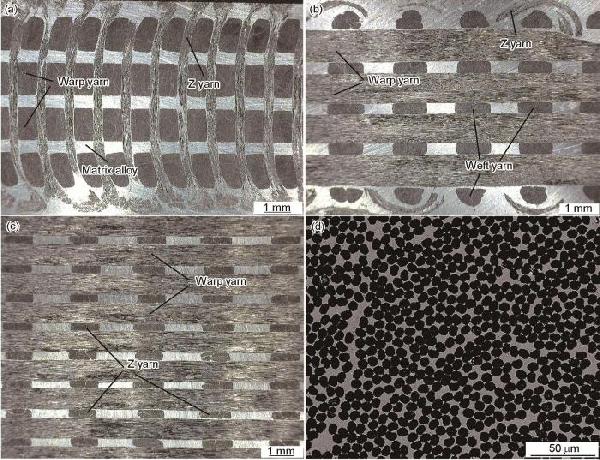
| 3D orthogonal | 200×250×4 |
Warp:12 Weft:5 |
Warp yarn:M40 6K×3 Weft yarn:M40 6K×2 Z yarn:M40 6K×1 |
0.975 |
50 |



| /MPa Em | νm |
σym /MPa |
EHm /MPa |
σum /MPa |
ε0pl /% |
εfpl /% |
|---|---|---|---|---|---|---|
| 81700 | 0.33 | 79.0 | 24900 | 130.0 | 0.16 | 0.80 |
| E11f/GPa | E22f/GPa | υ12f | υ23f | G12f/GPa | G23f/GPa | Xtf/MPa | Xcf/MPa |
|---|---|---|---|---|---|---|---|
| 377 | 19 | 0.26 | 0.3 | 8.9 | 7.3 | 1760 | 900 |
| E11/MPa | E22/MPa | G12/MPa | G23/MPa | ν12 | ν23 |
|---|---|---|---|---|---|
| 285460 | 21840 | 10120 | 8380 | 0.28 | 0.59 |
| Xt/MPa | Xc/MPa | Yt/MPa | Yc/MPa | S12/MPa | S23/MPa |
| 1240 | 750 | 34 | 112 | 100 | 16 |
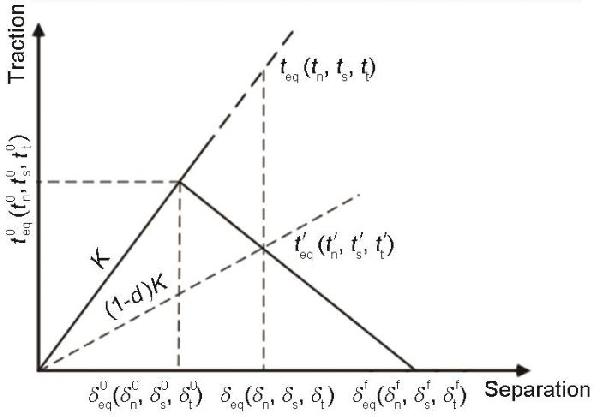
| tn0/MPa | ts0/MPa | tt0/MPa | Δˉ0/10-6m | Δˉf/10-6m |
|---|---|---|---|---|
| 16.0 | 9.5 | 9.5 | 0.08 | 0.72 |
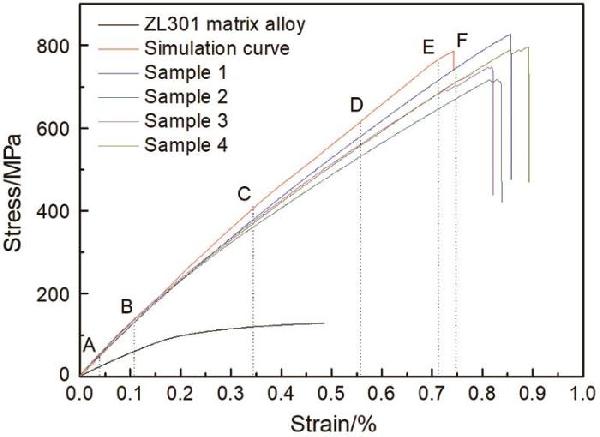
| Mechanical properties | Elastic moduli/GPa | Tensile strength/MPa | Fracture strain/% |
|---|---|---|---|
| Calculation | 116.82 | 785.32 | 0.75 |
| Experiments | 120.70 | 771.75 | 0.83 |
| Calculation error/% | -3.21 | 1.75 | -9.63 |
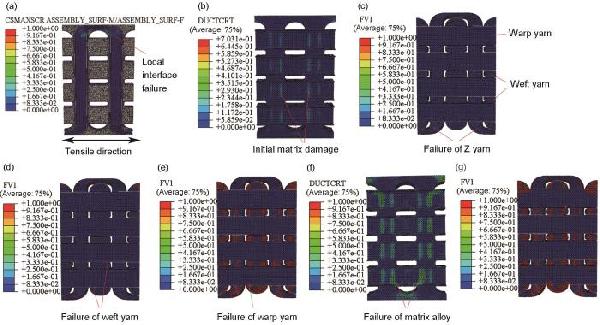

 分享 0
分享 0
 舉報 0
舉報 0
 收藏 0
收藏 0
 反對 0
反對 0
 點贊 0
點贊 0

 中冶有色技術(shù)平臺
中冶有色技術(shù)平臺 2024年12月27日 ~ 29日
2024年12月27日 ~ 29日  2024年12月27日 ~ 29日
2024年12月27日 ~ 29日  2025年01月03日 ~ 05日
2025年01月03日 ~ 05日  2025年01月03日 ~ 05日
2025年01月03日 ~ 05日  2025年04月27日 ~ 29日
2025年04月27日 ~ 29日 
