
全部
▼
搜索
熱搜:
位置:中冶有色 >
> 形狀因子對(duì)微觀定向結(jié)構(gòu)Cu-W復(fù)合材料觸頭的力學(xué)和電學(xué)性能的影響
 740
編輯:中冶有色技術(shù)網(wǎng)
來源:韓穎,李思達(dá),曹云東,李述軍,陸艷君,孫寶玉
740
編輯:中冶有色技術(shù)網(wǎng)
來源:韓穎,李思達(dá),曹云東,李述軍,陸艷君,孫寶玉
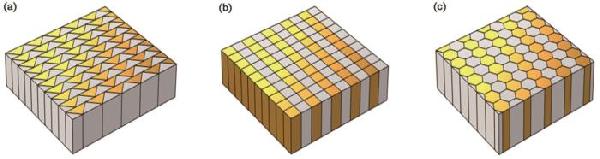
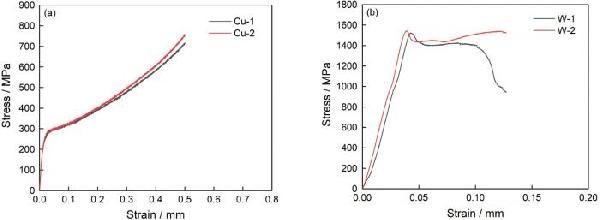







| 400 MPa | Triangle | Quadrilateral | Hexagon |
|---|---|---|---|
| Stress/MPa | 1.792×103 | 1.600×103 | 1.491×103 |
| Strain/mm | 1.416×10-2 | 1.353×10-2 | 1.312×10-2 |
 分享 0
分享 0
 舉報(bào) 0
舉報(bào) 0
 收藏 0
收藏 0
 反對(duì) 0
反對(duì) 0
 點(diǎn)贊 0
點(diǎn)贊 0

 中冶有色技術(shù)平臺(tái)
中冶有色技術(shù)平臺(tái) 2024年12月27日 ~ 29日
2024年12月27日 ~ 29日  2025年01月03日 ~ 05日
2025年01月03日 ~ 05日  2025年01月03日 ~ 05日
2025年01月03日 ~ 05日  2025年01月03日 ~ 05日
2025年01月03日 ~ 05日  2025年03月25日 ~ 27日
2025年03月25日 ~ 27日 
